20172313 2018-2019-1 《程序设计与数据结构》第七周学习总结
教材学习内容总结
- 概述
- 二叉查找树:二叉查找树是一种含有附加属性的二叉树,即其左孩子小于父结点,而父结点又小于或等于右孩子。二叉查找树的定义是二叉树定义的扩展。
- 二叉查找树的各种操作
| 操作 | 说明 | |
|---|---|---|
| addElement | 往树中添加一个元素 | |
| removeElement | 从树中删除一个元素 | |
| removeAllOccurrences | 从树中删除所指定元素的任何存在 | |
| removeMin | 删除树中的最小元素 | |
| removeMax | 删除树中的最大元素 | |
| findMin | 返回一个指向树中最小元素的引用 | |
| findMax | 返回一个指向树中最大元素的引用 |
- 用链表实现二叉查找树:每个BinaryTreeNode对象要维护一个指向结点所存储元素的引用,另外还要维护指向结点的每个孩子的引用。
- addElement操作:我们只要利用二叉查找树的特性(即对每个父结点,它的左子树中所有项的值小于父结点中的值,而它的右子树中所有项的值都大于T中的值),找到只对应的插入位置即可,如果树为空,则这个新元素就将成为新结点,如果树非空,沿着树查找(根据element的大小来判断向左还是向右)。假如我们现在要插入element为4的结点,如果找到element(4),则什么也不做,否则将element插入到遍历的路径上的最后一个点,如下图所示:

- removeElement操作:对于二叉查找树来说,删除元素的时候要考虑三种情况:
- ①如果要删除的结点q恰好是叶子结点,那么它可以立即被删除
- ② 如果要删除的结点q拥有一个孩子结点,则应该调整要被删除的父结点(p.left 或 p.right)指向被删除结点的孩子结点(q.left 或 q.right)
- ③如果要删除的结点q拥有两个孩子结点,则删除策略是用q的右子树的最小的数据替代要被删除结点的数据,并递归删除用于替换的结点(此时该结点已为空),此时二叉查找树的结构并不会被打乱,其特性仍旧生效。采用这样策略的主要原因是右子树的最小结点的数据替换要被删除的结点后可以满足维持二叉查找树的结构和特性,又因为右子树最小结点不可能有左孩子,删除起来也相对简单些。
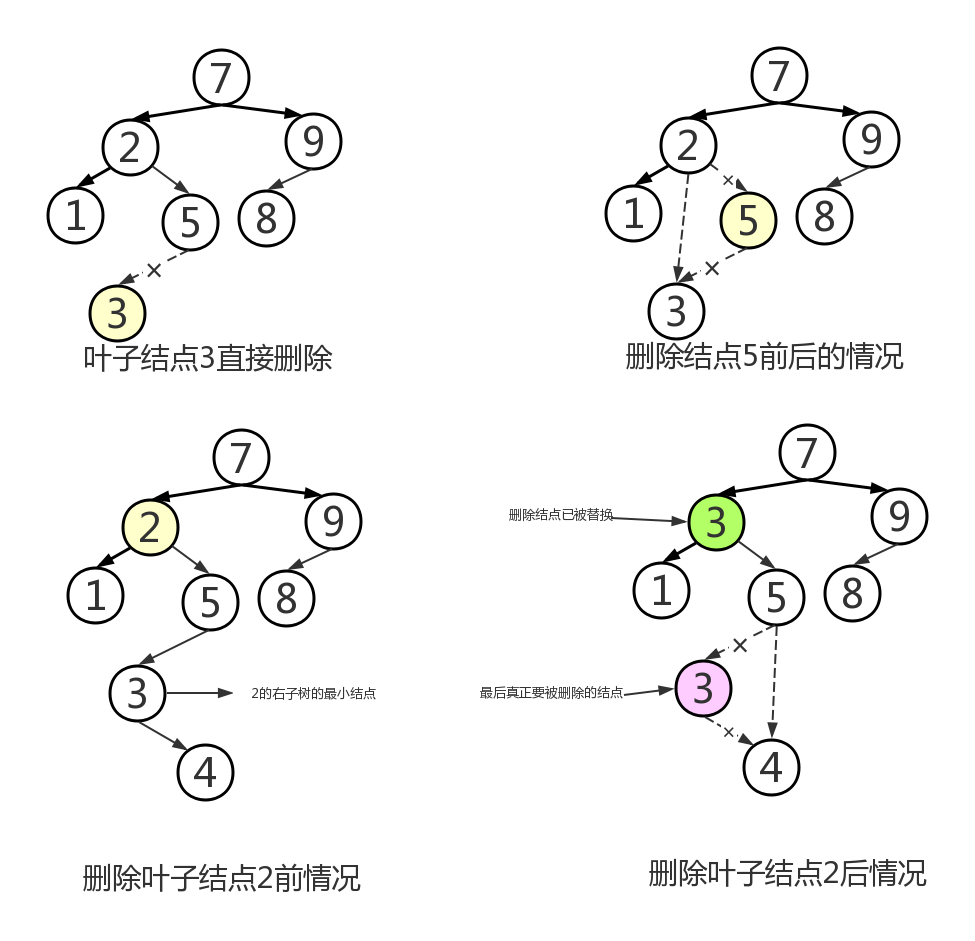
- removeAllOccurrences操作:可以看做调用了removeElement,当在树中找不到指定元素是,则抛出ElementNotFoundException异常,如果指定的元素不是Comparable,则removeAllOccurrences方法也会抛出ClassCaseException异常。只要树中还含有目标元素,就会再次调用removeElement方法。
public void removeAllOccurrences(T targetElement) throws ElementNotFoundException { removeElement(targetElement); try { while (contains((T)targetElement)) removeElement(targetElement); } catch (Exception ElementNotFoundException) { } } - removeMin和removeMax操作:对于findMin(),则需要从根结点开始并且只要有左孩子就向左进行即可,其终止点即为最小值的元素;而对于findMax(),也需要从根结点开始并且只要有右孩子就向右进行即可,终止点即为值最大的元素。
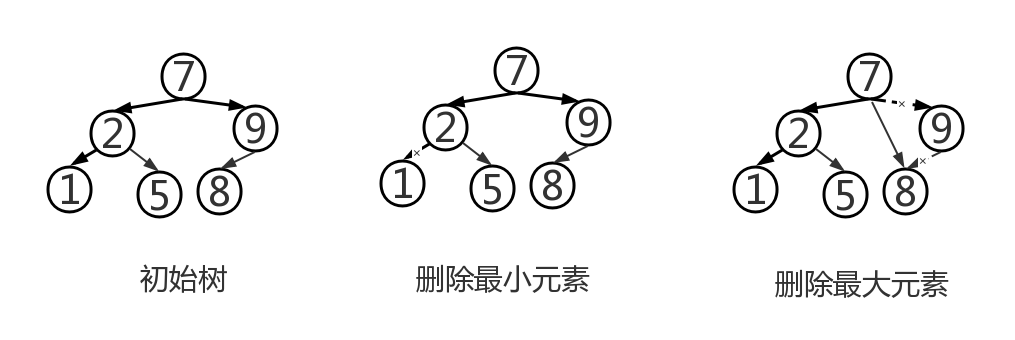
- 用有序列表实现二叉查找树:add操作和remove操作都可能导致树变得不平衡。
| 操作 | 说明 | LinkedList | BinarySearchTreeList |
|---|---|---|---|
| removeFirst | 删除列表的首元素 | O(1) | O(logn) |
| removeLast | 删除列表的末元素 | O(n) | (logn) |
| remove | 删除列表中的一个特定元素 | O(n) | O(logn)* |
| first | 考察列表前端的那个元素 | O(1) | O(logn) |
| last | 考察列表末端的那个元素 | O(n) | O(logn) |
| contains | 判断列表是否含有一个特定元素 | O(n) | O(logn) |
| is Empty | 判定列表是否为空 | O(1) | O(1) |
| size | 判定列表中的元素数目 | O(1) | O(1) |
| add(有序列表特有) | 向列表添加一个元素 | O(n) | O(logn)* |
- 平衡二叉查找树:如果没有平衡假设,最坏情况下addElement操作的实践复杂性是O(n)而不是O(logn),因为可能存在树根是树中的最小元素,而将被插入的元素可能是树中的最大元素,这种情况下,它的效率比链表的还低,因为每个结点还附带额外的开销。
- AVL树的旋转:当一棵树的最大路径长度大于log2^n,或最小路径长度小于log2^n-1时,就要平衡化该树。对于AVL树,树中的每一个结点,我们都会跟踪其左右子树的高度。对于树中的任何结点,如果其平衡因子(左右子树的高度差)大于1或小于-1,则以该节点为树根的子树需要重新平衡。
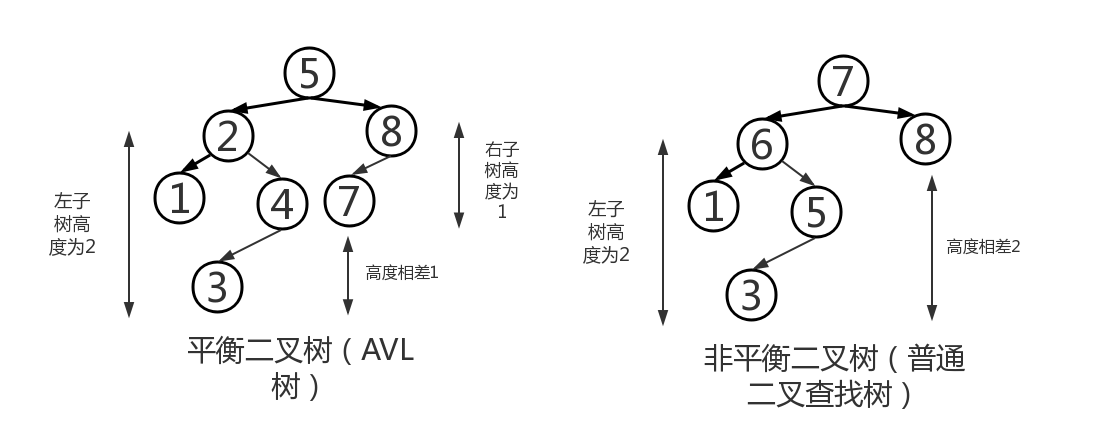
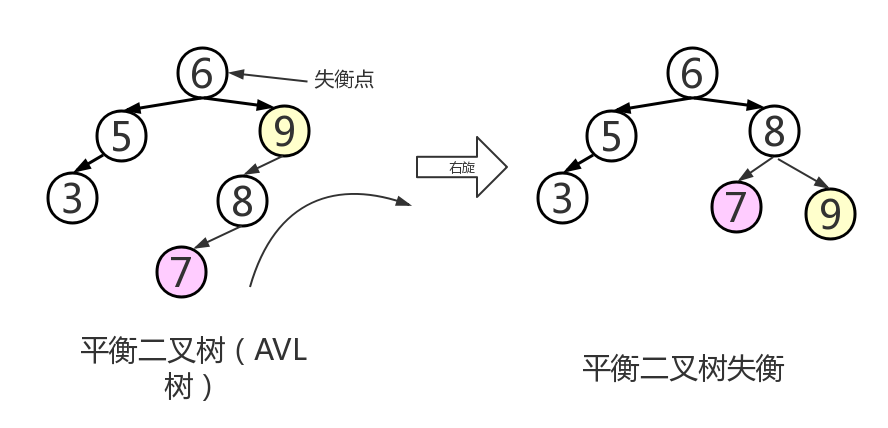
- 上左图是一棵平衡二叉树,它每个结点的左子树和右子树的高度最多相差1,它同时也是一棵二叉查找树,而上右图虽然也是一棵二叉查找树,但是它每个结点的左子树和右子树的高度相差为2,所以它不是平衡二叉树。当引起结点数量变化时,即进行删除和插入操作,如下图,插入一个新的结点,原本的平衡二叉树就失去了平衡。

- 既然二叉树失去了平衡,我们就要使用适当的操作来使它恢复平衡。如果某结点的平衡因子为-2,左孩子的平衡因子是-1,这就意味着该结点的左子树中有一条过长的路径,所以应该采用右旋。在原始AVL树插入7结点后,结点9变为失衡点,树再满足AVL性质,因此需要对9结点进行左左单旋转(即向右旋转)后,得到下右图,我们发现此时并没有操作树的根结点(6),实际上这是因为正常情况下,不必从树的根结点进行旋转,而是从插入结点处开始,向上遍历树,并更新和修复在这个路径上的每个结点的平衡及其平衡信息(高度)即可。(左旋类似,当某结点的平衡因子是+2,右孩子的平衡因子是+1的时候使用左旋,左旋中的“左”,意味着“被旋转的结点将变成一个左结点”。右旋同理)
- 当某结点的平衡因子是+2,如果其右孩子的平衡因子是-1,这时子树太“深”了,无论是左旋还是右旋,都无法使操作后的数成为AVL树,这个时候就需要使用双旋,首先让出初始结点右孩子的左孩子,绕着初始结点的右孩子进行一次右旋,然后再让初始结点的右孩子,绕着初始结点进行一次左旋。(左右旋类似,当某结点的平衡因子是-2,左孩子的平衡因子是+1的时候使用左右旋)

- 红黑树
- 树中的每一个结点都储存着一种颜色(红色或黑色,通常使用一个布尔值来实现,值false等价于红色)。
- 根结点为黑色。
- 每个叶子结点(null)是黑色。(**注意:这里的叶子结点,是指为空(null)的叶子结点!)
- 从树根到树叶的每条路径都包含有同样数目的黑色结点。
- 如果一个结点的颜色为红色,那么它的子结点必定是黑色。
- 在红黑树中,元素的查找仍然是一种O(n)操作,由于红色结点不能有红色孩子,于是路径中至多有一半结点时红色结点、至少有一半结点是黑色结点,据此我们可以论证红黑树的最大高度约为2*logn,于是遍历最长路径的序仍然是logn。

- 红黑树的添加操作:红黑树本身就是一棵二叉查找树,所以当添加元素或删除元素后,我们仍然需要使所得到的是一棵二叉查找树,这就使得我们要对红黑树进行重新着色。我们先来回头看上面所说的红黑树的性质,如果要保证从树根到树叶的每条路径都包含有同样数目的黑色结点,那么我们把插入的元素设置为红色,就可以保持,接下来我们只需从该结点向上遍历,保证红色结点的子结点必定为黑色即可满足红黑树的所有要求。我们把要插入的结点设置为红色,那么根据父结点的颜色又可以分为三种情况。
- ①被插入的结点是根结点。(我们可以直接将该结点涂成黑色)
- ②被插入的结点的父结点是黑色。 (我们无需进行操作,插入之后仍为红黑树)
- ③被插入的结点的父结点是红色。(我们对该种情况要进行着重讨论,因为被插入的结点的父结点是红色,所以该结点的祖父结点必定存在(即父结点的父结点),父结点的兄弟结点也必定存在。(即“叔叔”结点,即使叔叔结点为空,我们也视之为存在,空结点本身就是黑色结点)我们根据叔叔结点的颜色又可以分成三种情况)
| 情况 | 处理方式 |
|---|---|
| 当前结点的父结点是红色,且当前结点的祖父结点的另一个子结点(叔叔结点)也是红色。 | ①将“父结点”设为黑色。② 将“叔叔结点”设为黑色。③ 将“祖父结点”设为“红色”。④ 将“祖父结点”设为“当前结点”(红色结点);指针current由指向插入的结点变为“当前结点“”,之后继续对“当前结点”向上进行操作。 |
| 当前结点的父结点是红色,叔叔结点是黑色,且当前结点是其父结点的右孩子 | ①将“父结点”作为“新的当前结点”。②以“新的当前结点”为支点进行左旋。 |
| 当前结点的父结点是红色,叔叔结点是黑色,且当前结点是其父结点的左孩子 | ① 将“父节点”设为“黑色”。②将“祖父节点”设为“红色”。③以“祖父结点”为支点进行右旋。 |
- 如上图介绍了如何进行操作,下面我们再来谈谈为什么要这么操作。
- 第一种情况,由于红色结点的子结点不能是红色,所以我们把父结点要变为黑色,但当我们把父结点变为黑色以后,从树根到树叶之间的黑色结点的个数就不相等了,所以把祖父结点变为红色,同样的,因为红色结点的子孩子不能是红色,所以要把叔叔结点变为黑色。祖父结点一定是黑色吗?答案是肯定的,因为在元素添加之前,该二叉树就是红黑树,父结点是红色的,那么祖父结点一定是黑色的。按照上述步骤处理之后,当前结点,父结点,叔叔结点都满足了红黑树的性质。若此时,祖父结点是根结点,直接将祖父结点设为“黑色”,那就完全解决这个问题了;若祖父结点不是根结点,那我们需要将“祖父结点”设为“新的当前结点”,接着对“新的当前结点”进行分析。
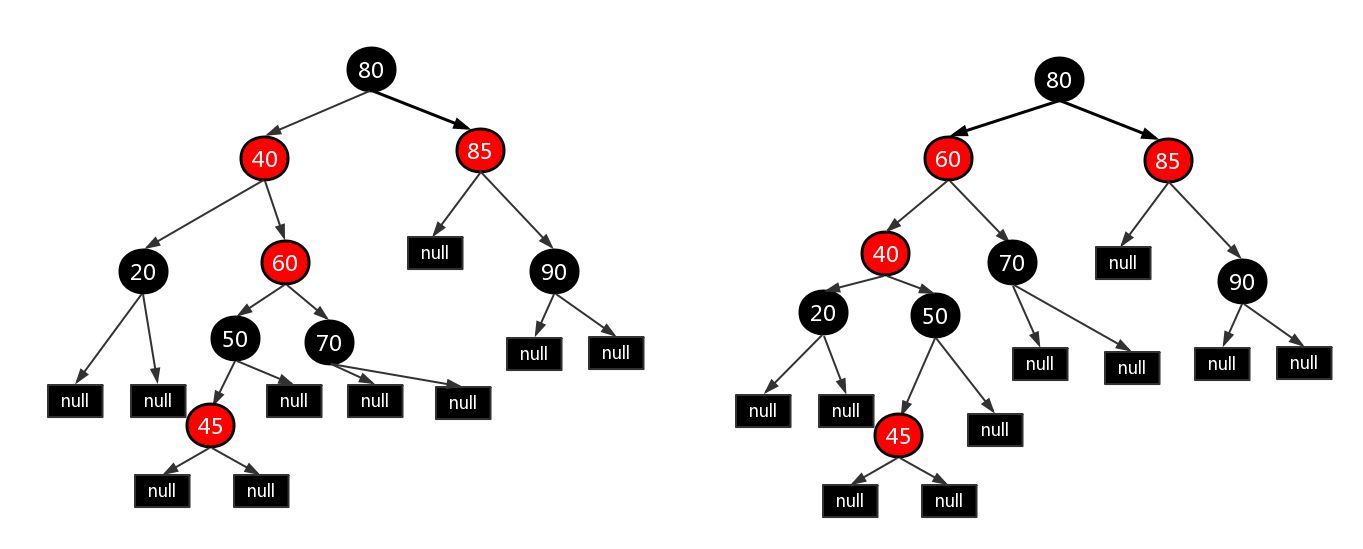
- 第二种情况,我们在上面表中说到,要以父结点为支点进行左旋,那么为什么要进行左旋呢?处理红黑树的核心思想:将红色的结点移到根节点;然后,将根结点设为黑色。新插入的结点为红色,破坏了整棵红黑树,所以我们要通过左旋来将它上移。上移之后,如果该结点变成了根结点,那么直接把它涂成黑色,若该结点不是 根结点,那么我们需要对父结点进行操作(在下图中也就是40) ,为什么不直接对60的当前结点进行操作,而是转而处理原来的父结点40呢?因为通过左旋之后,原来的父结点(40)变成了子结点(60)的子结点,而处理红黑树的时候需要从下往上处理,所以要先对40的结点操作。
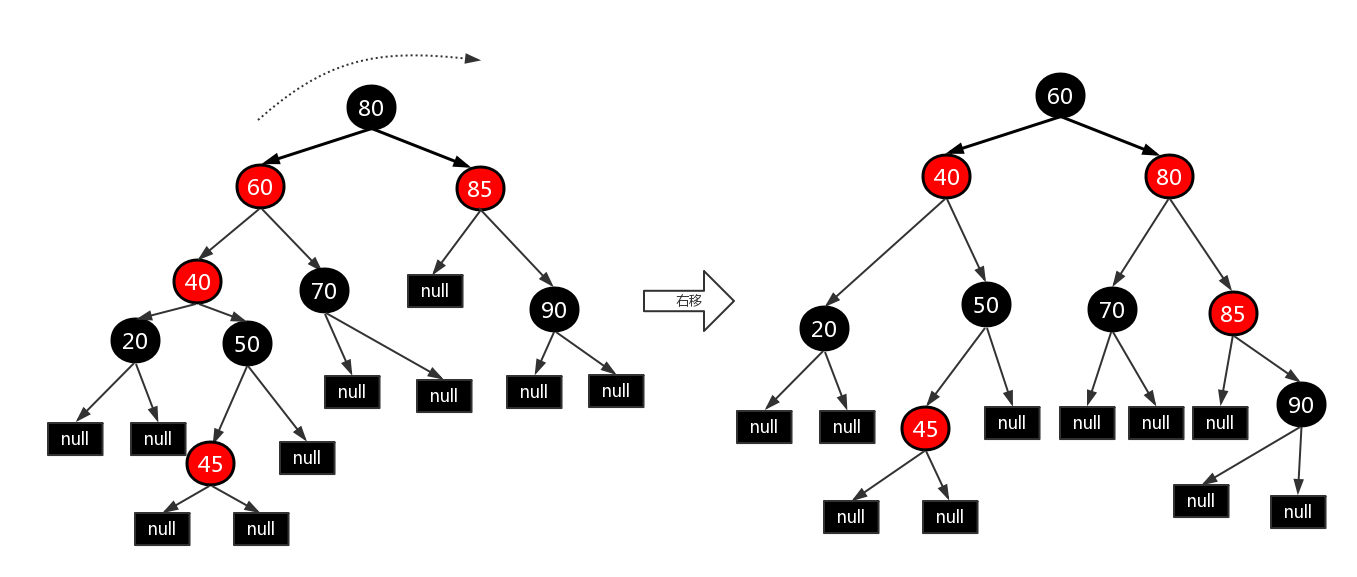
- 第三种情况,当按照上图第二种情况左旋后,就变成了下面这种情况。由于(40)和(60)两个结点都是红色,所以我们可以先把(60)结点变为黑色,但变为黑色的话,由根结点经过(60)结点的路径黑色结点数就会增加,所以我们可以让(60)的父结点(即(80))变为红色,并以该父结点作为支点进行右旋。
- 红黑树的删除操作:红黑树的删除和常规二叉树删除元素的操作一样,也分为三种情况。
- ①被删除的结点没有子结点(即叶子节点),直接将该结点删除。
- ②被删除的结点有一个子结点,将该结点删除,并让父结点指向该结点的子结点。(可以看前文的示意图)
- ③被删除的结点有两个子结点,用该结点的右子树的最小的数据替代要被删除结点的数据,并递归删除用于替换的结点。(前文有,在此不再过多赘述)
- 在删除结点的时候,我们还要考虑到结点的颜色问题,当删除的结点颜色是红色时,直接按照上述操作拿孩子结点填补空位即可,因为删除红色结点不会影响黑色结点的数量。如果要删除的结点的颜色为黑色,为了保持黑色结点数量的一致,如果该结点的孩子结点为红色,那么把孩子结点变为红色并拿来填补空位即可。如果孩子结点为黑色,情况就复杂得多,我们在下面再细细探讨。在这里先来统一一下下文字母代表的含义。这里假设最终被删除的节点为X(至多只有一个孩子节点,可以有两个,但演示的时候没必要),其孩子结点为N,X的兄弟结点为S,S的左结点为 SL,右结点为 SR。接下来讨论是建立在结点 X 被删除,结点 N 替换X的基础上进行的。
- ①要删除的结点X为根结点,且无左右孩子结点,直接删除。
- ②S结点为红色,其它结点为黑色,这种情况下可以对 N 的父节点进行左旋操作,然后互换 P 与 S 颜色。但经过节点 P 和 N 的路径删除前有3个黑色节点(P -> X -> N),现在只剩两个了(P -> N)。比未经过 N 的路径少一个黑色节点,此时从根节点到各路径的黑色结点数量不同,然后可以使用下面四、五、六种情况进行处理。
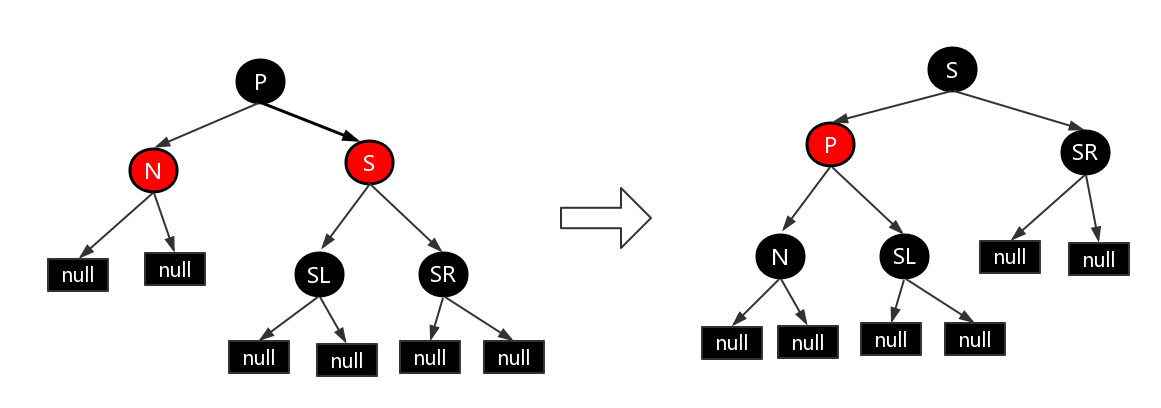
- ③N 的父结点,兄弟结点 S 和 S 的孩子结点均为黑色。这种情况下可以简单的把 S 染成红色,所有经过 S 的路径比之前少了一个黑色结点,这样经过 N 的路径和经过 S 的路径黑色结点数量一致了。但经过 P 的路径比不经过 P 的路径少一个黑色结点,此时需要从情况一开始对 P 进行平衡处理。
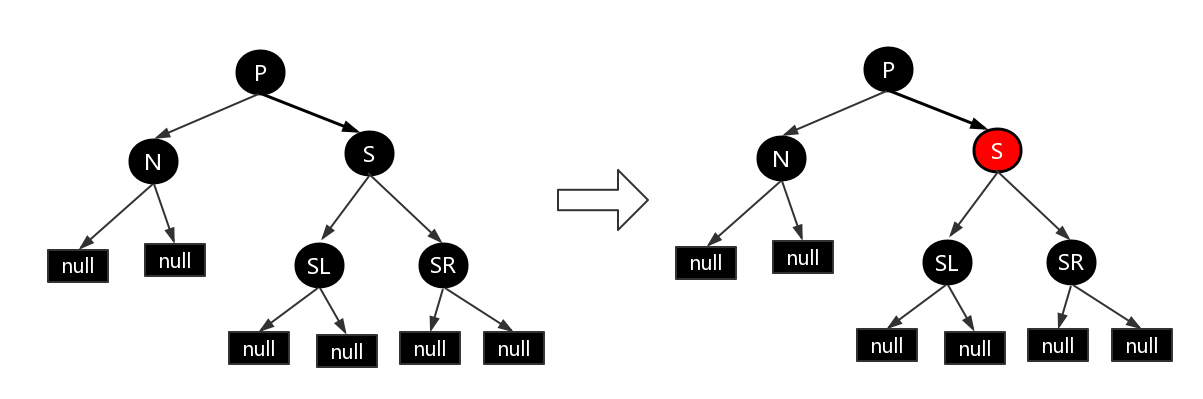
- ④N 的父节点是红色,S 和 S 孩子为黑色。这种情况比较简单,我们只需交换 P 和 S 颜色即可。这样所有通过 N 的路径上增加了一个黑色节点,所有通过 S 的节点的路径必然也通过 P 节点,由于 P 与 S 只是互换颜色,并不影响这些路径。
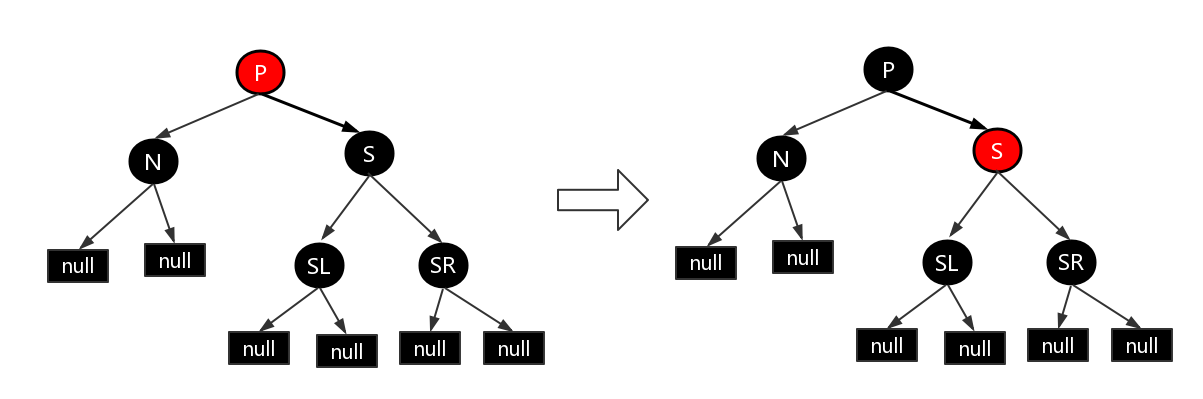
- ⑤S 为黑色,S 的左孩子为红色,右孩子为黑色。N 的父节点颜色可红可黑,且 N 是 P 左孩子。这种情况下对 S 进行右旋操作,并互换 S 和 SL 的颜色。此时,所有路径上的黑色数量仍然相等,N 兄弟节点的由 S 变为了 SL,而 SL 的右孩子变为红色。接下来我们到情况六继续分析。
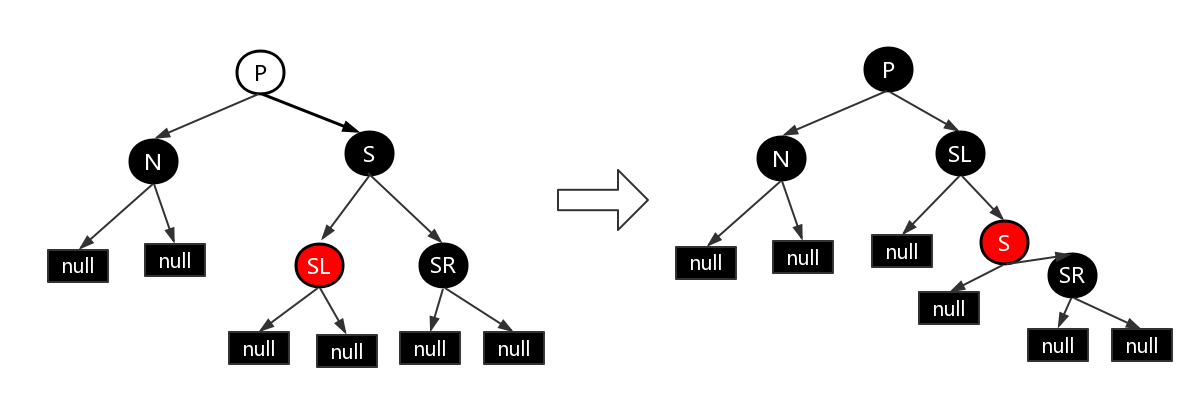
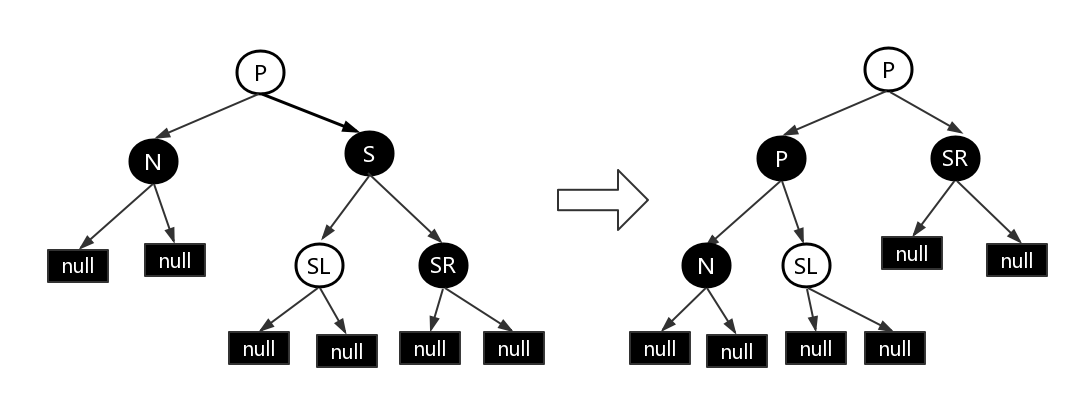
- ⑥S 为黑色,S 的右孩子为红色。N 的父节点颜色可红可黑,且 N 是其父节点左孩子。这种情况下,我们对 P 进行左旋操作,并互换 P 和 S 的颜色,并将 SR 变为黑色。因为 P 变为黑色,所以经过 N 的路径多了一个黑色节点,经过 N 的路径上的黑色节点与删除前的数量一致。对于不经过 N 的路径,则有以下两种情况:
- 该路径经过 N 新的兄弟节点 SL ,那它之前必然经过 S 和 P。而 S 和 P 现在只是交换颜色,对于经过 SL 的路径不影响。
- 该路径经过 N 新的叔叔节点 SR,那它之前必然经过 P、 S 和 SR,而现在它只经过 S 和 SR。在对 P 进行左旋,并与 S 换色后,经过 SR 的路径少了一个黑色节点,性质5被打破。另外,由于 S 的颜色可红可黑,如果 S 是红色的话,会与 SR 形成连续的红色节点,打破性质4(每个红色节点必须有两个黑色的子节点)。此时仅需将 SR 由红色变为黑色即可同时恢复性质4和性质5(从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。)。
教材学习中的问题和解决过程
- 问题一:在学习教材的时候,p225的代码中有这样一行判断条件“(!(element instanceof Comparable))”,不是很理解这行代码的意思。
- 问题一解决方法:原来是学习过的,时间久了有些忘记。java 中的instanceof 运算符是用来在运行时指出对象是否是特定类的一个实例。instanceof通过返回一个布尔值来指出,这个对象是否是这个特定类或者是它的子类的一个实例。用法:result = object instanceof class参数:Result:布尔类型。Object:必选项。任意对象表达式。Class:必选项。任意已定义的对象类。说明:如果 object 是 class 的一个实例,则 instanceof 运算符返回 true。如果 object 不是指定类的一个实例,或者 object 是 null,则返回 false。 举例:
interface A{} class B implements A{ } class C extends B { } class instanceoftest { public static void main(String[] args){ A a=null; B b=null; boolean res; System.out.println("instanceoftest test case 1: ------------------"); res = a instanceof A; System.out.println("a instanceof A: " + res); res = b instanceof B; System.out.println("b instanceof B: " + res); System.out.println("/ninstanceoftest test case 2: ------------------"); a=new B(); b=new B(); res = a instanceof A; System.out.println("a instanceof A: " + res); res = a instanceof B; System.out.println("a instanceof B: " + res); res = b instanceof A; System.out.println("b instanceof A: " + res); res = b instanceof B; System.out.println("b instanceof B: " + res); System.out.println("/ninstanceoftest test case 3: ------------------"); B b2=(C)new C(); res = b2 instanceof A; System.out.println("b2 instanceof A: " + res); res = b2 instanceof B; System.out.println("b2 instanceof B: " + res); res = b2 instanceof C; System.out.println("b2 instanceof C: " + res); } } 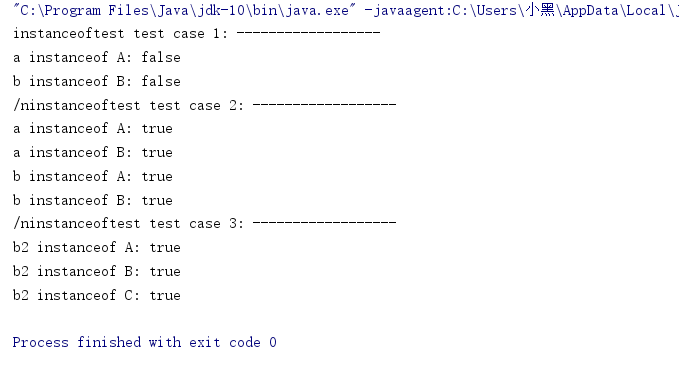
- 问题二:对于红黑树的添加和删除原理不是很理解。
- 问题二解决方法:在上方教材总结中体现。
代码调试中的问题和解决过程
- 问题一:在编写pp的时候,为了比较两个对象的大小,时常需要在类的头部声明“T extends Comparable”,那么代码泛型中T继承的Comparable到底是整个方法是Comparable类型还是其中的变量是Comparable类型。
- 问题一解决方法:
- 大家可以明白的是这里应用到了Java的泛型,那么首先向大家说明一下这里extends的作用extends后面跟的类型,如表示泛型的上限。示例代码如下:
import java.util.*;class Demo{}public class Test{ public static void main(String[] args) { Demo p = null; // 编译正确//这里因为ArrayList是List的子类所以通过//如果改为Demo p = null;就会报错这样就限制了上限 }}
- 在理解了extends所表示的泛型的上限后,接下来介绍一下super的作用,它与extends相反,表示的是泛型的下限。所以结合上述两点,我们来分析一下这句话整体代表什么意思。首先,extends对泛型上限进行了限制即T必须是Comparable<? super T>的子类,然后<? super T>表示Comparable<>中的类型下限为T!那么 <T extends Comparable> 和 <T extends Comparable<? super T>> 到底有什么不同呢?
- 我们首先来理解<T extends Comparable>的含义,它代表的意思是:类型T必须实现Comparable接口,并且这个接口的类型是T。这样,T的实例之间才能相互比较大小。这边我们以Java中GregorianCalendar这个类为例。代码如下所示:
import java.util.GregorianCalendar;class Demo>{}//注意这里是没有? super的public class Test{ public static void main(String[] args) { Demo p = null; }}
- 这里编译报错,因为这里的<T extends Comparable>相当于<GregorianCalendar extends Comparable>,但是GregorianCalendar中并没有实现Comparable,而是仅仅持有从Calendar继承过来的Comparable,这样就会因为不在限制范围内而报错。
- 我们接下来再来看看<T extends Comparable<? super T>>的含义。它代表的意思是:类型T必须实现Comparable接口,并且这个接口的类型是T或者是T的任一父类。这样声明后,T的实例之间和T的父类的实例之间可以相互比较大小。同样还是以GregorianCalendar为例。代码如下所示:
import java.util.GregorianCalendar; class Demo<T extends Comparable<? super T>>{} public class Test1 { public static void main(String[] args) { Demo<GregorianCalendar> p = null; // 编译正确 } }
- 此时编译通过,这里可以理解为<GregorianCalendar extends Comparable>!因为Calendar为GregorianCalendar 的父类并且GregorianCalendar 实现了Comparable>。
- 问题二:在学习红黑树的时候,书上提到终止迭代的条件也可以是“current.parent.color == black”,子树的结点不也可以是黑色的吗?为什么判断当前结点的父结点的颜色就可以终止迭代了呢?
- 问题二解决方法:这里是我没有好好理解红黑树,对书上的解释没有弄明白。因为插入的结点为红色,要根据父结点和叔叔结点的颜色进行操作并自下而上进行迭代,当当前结点的父结点为红色时,这时候整个二叉树已经满足红黑树的所有特性,所以可以不在进行操作。(具体操作在前文中有细致体现)

上周考试错题总结
这周没有错题哦~
结对及互评
- 博客中值得学习的或问题:
- 排版精美,对教材的总结细致,善于发现问题,对于问题研究得很细致,解答也很周全。
- 代码中值得学习的或问题:
- 代码写的很规范,思路很清晰,继续加油!
点评过的同学博客和代码
- 本周结对学习情况
- 结对学习内容
- 第11章 二叉查找树
- 结对学习内容
其他(感悟、思考等,可选)
这周的内容还是比较难得,不难在代码上,难在内容的理解和理清它们之间的关系,根据不同的情况进行不同的操作,上周由于刚刚接触学习树,所以在代码的理解上花费不少时间,这周主要是上网查询了不少资料来弄明白各种情况。但这周的学习时间并没有减少,相反,我觉得比上周还要吃力,但学习完之后还是明显能够感觉到自己的进步的,希望能在以后的学习生活中继续努力,继续进步吧!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 第一周 | 200/200 | 1/1 | 5/20 | |
| 第二周 | 981/1181 | 1/2 | 15/20 | |
| 第三周 | 1694/2875 | 1/3 | 15/35 | |
| 第四周 | 3129/6004 | 1/4 | 15/50 | |
| 第五周 | 1294/7298 | 1/5 | 15/65 | |
| 第六周 | 1426/8724 | 1/6 | 20/85 | |
| 第七周 | 2071/10795 | 1/7 | 20/105 |
计划学习时间:20小时
实际学习时间:20小时